Gaussian Beams Calculator

View All Technical Tools

Axial Distance, $ z \left[ \text{mm} \right] $:

Beam Waist, $ \omega_0 \left[ \text{mm} \right] $:

Wavelength, $ \lambda [ \large{\unicode[computer modern]{x03BC}} \text{m} ] $:

Half Beam Diameter, $ \omega \! \left( z \right) \left[ \text{mm} \right] $: --

Radius of Curvature, $ R \! \left( z \right) \left[ \text{mm} \right] $: --

Rayleigh Range, $ Z_R \left[ \text{mm} \right] $: --

Rayleigh Half Diameter, $ \omega_R \left[ \text{mm} \right] $: --

Half Angle Divergence, $ \theta \left[ \text{mrad} \right] $: --

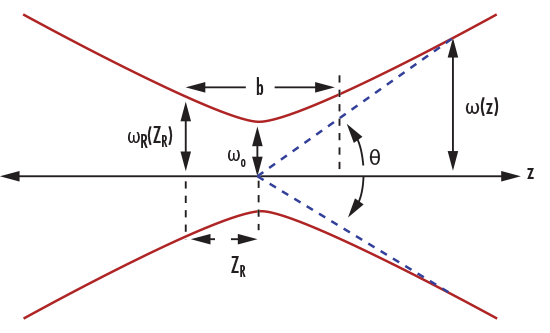
$$ z_R = \frac{\pi \omega_0 ^2}{\lambda} $$	$$ \omega \! \left( z \right) = \omega_0 \sqrt{1 + \left( \frac{z}{z_R} \right) ^2} $$	$$ Z_R = \frac{b}{2} $$
$$ \omega_R = \omega \! \left( Z_R \right) = \sqrt{2} \cdot \omega_0 $$	$$ R \! \left( z \right) = z \left[ 1 + \left( \frac{z_R}{z} \right)^2 \right] $$	$$ \theta = \frac{\lambda}{\pi \, \omega_0} $$

$$ \lambda $$	Wavelength
_{$$ Z_R $$}	Rayleigh Range
$$ z $$	Axial Distance
$$ \omega \! \left( z \right) $$	Half Beam Diameter
$$ \omega_0 $$	Beam Waist

$$ b $$	Confocal Parameter
$$ \omega_R $$	Rayleigh Half Diameter
$$ R \! \left( z \right) $$	Radius of Curvature
$$ \theta $$	Half Angle Divergence

Notes:

Please use the American standard for number formatting rather than the European standard (i.e. for "two and a half," enter "2.5" rather than "2,5").
Results greater than 1,000,000 are rounded to infinity.

Description

Mathematically model beam propagation of Gaussian beam using simple geometric parameters. Calculator uses first-order approximations and assumes TEM₀₀ mode to determine beam spot size in free space applications. Please note that results will vary based on beam quality and application conditions.