Importance of Beam Diameter on Laser Damage Threshold
This is Section 14.7 of the Laser Optics Resource Guide.
The diameter of a laser highly affects an optic’s laser-induced damage threshold (LIDT) as beam diameter directly influences the probability of laser-induced damage.1 When the beam size of a laser used for LIDT testing is significantly larger than the density of defects on the optic, the likelihood of triggering scarce damage mechanisms is high - these unlikely events are detectable. If the beam size is too small, low defect densities are not always detectable and parts appear more resistant to damage than they actually are (Figure 1).

Figure 1: Small diameter beams are less likely to overlap with low density defects on an optic undergoing testing, resulting in overly-optimistic LIDT values
The smallest beam diameter permitted for LIDT testing in ISO 21254 is 0.2mm. Many laser optics suppliers prefer to use as small of a beam as possible because it is easier to achieve a high fluence, although this may lead to an “under-sampling” of the surface. Figure 2 demonstrates how laser damage scales with the diameter of a beam. In the scenario shown, a large number of the defects have a threshold fluence of 10J and a small number have a threshold fluence of 1J. This simplified model provides insight for real world usage, as laser optics typically contain various types of defects with different densities and individual damage thresholds. Scaling the beam diameter from 0.2mm to 10mm will drastically change the damage probability function and therefore change the LIDT value concluded from the test. With a 0.2mm beam, the chance of detecting one of the 1J threshold defects is small. For this reason, the damage probability will remain very low until a fluence of 10J is reached. Increasing the beam size from 0.2mm to 2mm makes detecting 1J threshold defects more likely, thereby causing a sharp increase in damage probability at a fluence of 1J. When the beam diameter is scaled to 10mm, the damage probability at 1J increases to an almost certain probability of damage.
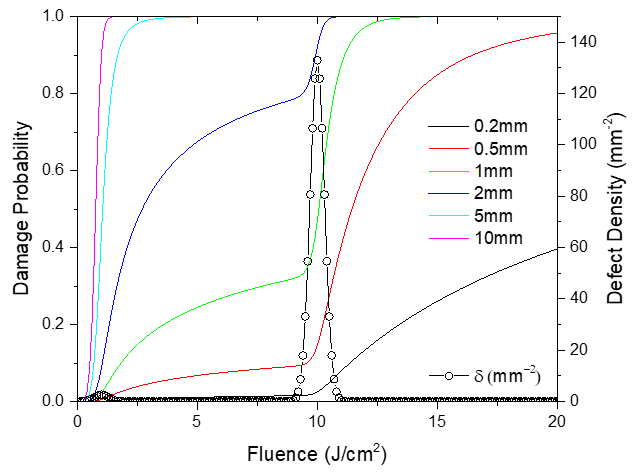
Figure 2: In this example with 2 different defect types, LIDT drops by a factor of 10 when scaling the beam size from 0.2mm to 10mm
While LIDT scales with changes in wavelength and pulse duration, it also scales with beam diameter. For small changes in beam diameter, this scaling can be approximated by multiplying the original LIDT value by the square of the ratio of the original diameter to the new diameter.1
Equation 1 approximates the shift of an LIDT at an initial wavelength (λ1), pulse duration (τ1), and beam diameter (∅1) to a new wavelength (λ2), pulse duration (τ2), and beam diameter (∅1). Our Laser Induced Damage Threshold Scaling Calculator provides approximations for scaling an LIDT value for small shifts in beam diameter and the other application conditions.
Reference
- L. Gallais, J. Capoulade, J.-Y. Natoli and M. Commandré, "Investigation of nanodefect properties in optical coatings by coupling measured and simulated laser damage statistics," J. Appl. Phys, vol. 104, p. 053120, 2008.
More Resources
- Understanding and Specifying LIDT of Laser Components Application Note
- Laser Damage Threshold Testing Application Note
- Laser Damage Threshold Scaling Calculator
- Uncertainty in LIDT Specifications Application Note
- Different Types of LIDT Specifications Application Note
- Bulk Laser Damage in Glass Application Note
- LIDT for Ultrafast Lasers Application Note
- Why Laser Damage Testing is Critical for UV Laser Applications Application Note
- A Guide to (Not Over) Specifying Losses in Laser Optics Application Note
- Metrology at Edmund Optics: Measuring as a Key Component of Manufacturing Video
- Metrology for Laser Optics Application Note
- Key Parameters of a Laser System Application Note
- Laser Optics Lab Video Series













 Previous Section
Previous Section 




















































































or view regional numbers
QUOTE TOOL
enter stock numbers to begin
Copyright 2023 | Edmund Optics, Ltd Unit 1, Opus Avenue, Nether Poppleton, York, YO26 6BL, UK
California Consumer Privacy Acts (CCPA): Do Not Sell or Share My Personal Information
California Transparency in Supply Chains Act