Gaussian Beam Propagation
This is Section 2.1 of the Laser Optics Resource Guide.
In many laser optics applications, the laser beam is assumed to be Gaussian with an irradiance profile that follows an ideal Gaussian distribution. All actual laser beams will have some deviation from ideal Gaussian behavior. The M2 factor, also known as the beam quality factor, compares the performance of a real laser beam with that of a diffraction-limited Gaussian beam.1 Gaussian irradiance profiles are symmetric around the center of the beam and decrease as the distance from the center of the beam perpendicular to the direction of propagation increases (Figure 1). This distribution is described by Equation 12:
In Equation 1, I0 is the peak irradiance at the center of the beam, r is the radial distance away from the axis, w(z) is the radius of the laser beam where the irradiance is 1/e2 (13.5%) of I0, z is the distance propagated from the plane where the wavefront is flat, and P is the total power of the beam.
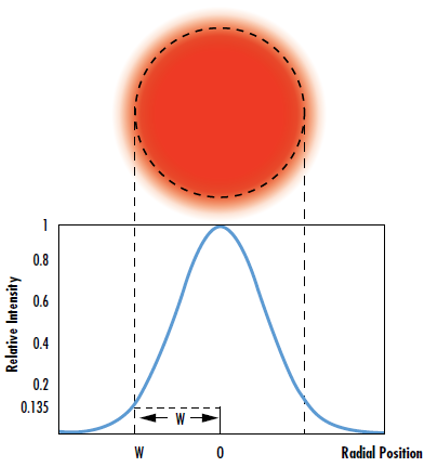
Figure 1: The waist of a Gaussian beam is defined as the location where the irradiance is 1/e2 (13.5%) of its maximum value
However, this irradiance profile does not stay constant as the beam propagates through space, hence the dependence of w(z) on z. Due to diffraction, a Gaussian beam will converge and diverge from an area called the beam waist (w0), which is where the beam diameter reaches a minimum value. The beam converges and diverges equally on both sides of the beam waist by the divergence angle θ (Figure 2). The beam waist and divergence angle are both measured from the axis and their relationship can be seen in Equation 2 and Equation 32:
In the above equations, λ is the wavelength of the laser and θ is a far field approximation. Therefore, θ does not accurately represent the divergence of the beam near the beam waist, but it becomes more accurate as the distance away from the beam waist increases. As seen in Equation 3, a small beam waist results in a larger divergence angle, while a large beam waist results in a smaller divergence angle (or a more collimated beam). This explains why laser beam expanders can reduce beam divergence by increasing beam diameter.
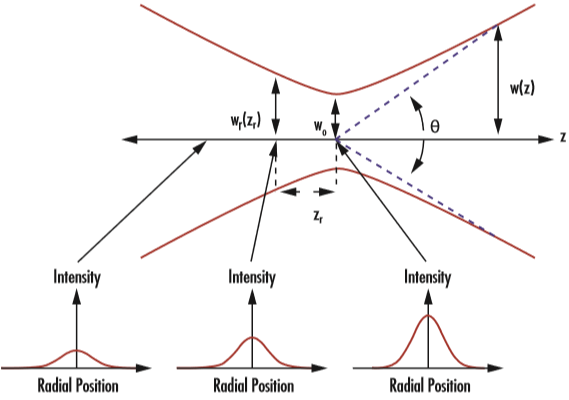
Figure 2: Gaussian beams are defined by their beam waist (w0), Rayleigh range (zR), and divergence angle (θ)
Variation of the beam diameter in the beam waist region is defined by:
The Rayleigh range of a Gaussian beam is defined as the value of z where the cross-sectional area of the beam is doubled. This occurs when w(z) has increased to √2 w0. Using Equation 4, the Rayleigh range (zR) can be expressed as:
This allows w(z) to also be related to zR:
The wavefront of the laser is planar at the beam waist and approaches that shape again as the distance from the beam waist region increases. This occurs because the radius of curvature of the wavefront begins to approach infinity. The radius of curvature of the wavefront decreases from infinity at the beam waist to a minimum value at the Rayleigh range, and then returns to infinity when it is far away from the laser (Figure 3); this is true for both sides of the beam waist.3
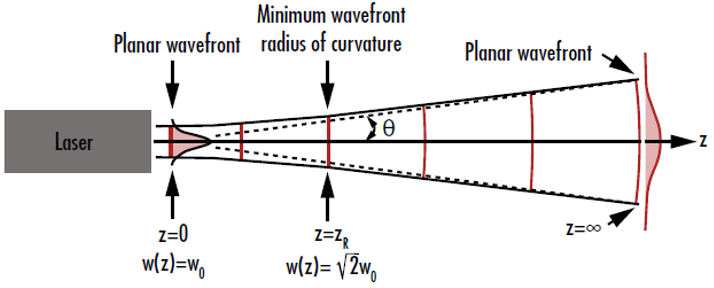
Figure 3: The curvature of the wavefront of a Gaussian beam is near-zero when it is both very close and very far away from the beam waist
Gaussian Beam Manipulation
Many laser optics systems require manipulation of a laser beam as opposed to simply using the “raw” beam. This may be done using optical components such as lenses, mirrors, prisms, etc. Below is a guide to some of the most common manipulations of Gaussian beams.
The Thin Lens Equation for Gaussian Beams
The behavior of an ideal thin lens can be described using the following equation2:
In Equation 7, s’ is the distance from the lens to the image, s is the distance from the lens to the object, and f is the focal length of the lens. If the object and image are at opposite sides of the lens, s is a negative value and s’ is a positive value. This equation ignores the thickness of a real lens and is therefore only a simple approximation of real behavior (Figure 4). The thin lens equation can also be written in a dimensionless form by multiplying both sides of the equation by f:
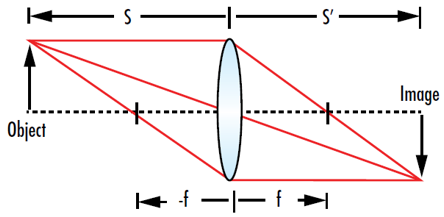
Figure 4: The thin lens equation allows the position of an image (s’) to be determined when the distance from the lens to the object (s) and the focal length of the lens (f) are known
In addition to describing imaging applications, the thin lens equation is applicable to the focusing of a Gaussian beam by treating the waist of the input beam as the object and the waist of the output beam as the image. Gaussian beams remain Gaussian after passing through an ideal lens with no aberrations. In 1983, Sidney Self developed a version of the thin lens equation that took Gaussian propagation into account4:
The total distance from the laser to the focused spot is calculated by adding the absolute value of s to s’. Equation 9 can also be written in a dimensionless form by multiplying both sides by f:
This equation approaches the standard thin lens equation as zR/f approaches 0, allowing the standard thin lens equation to be used for lenses with a long focal length. Equations 9 and 10 can be used to find the location of the beam waist after being imaged through the lens (Figure 5).
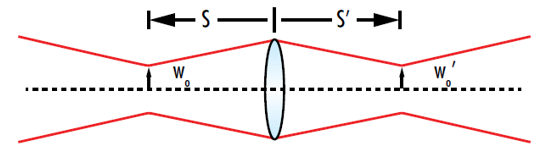
Figure 5: The ”object” when refocusing a Gaussian beam is the input waist and the “image” is the output waist
A plot of the normalized image distance (s’/f) versus the normalized object distance (s/f) shows the possible output waist locations at a given normalized Rayleigh range (zR/f) (Figure 6). This plot shows that Gaussian beams focused through a lens have a few key differences when compared to conventional thin lens imaging. Gaussian beam imaging has both minimum and maximum possible image distances, while conventional thin lens imaging does not. The maximum image distance of a refocused Gaussian beam occurs at an object distance of -(f + zR), as opposed to –f. The point on the plot where s/f is equal to -1 and s’/f is equal to 1 indicates that the output waist will be at the back focal point of the lens if the input is at the front focal point of a positive lens.
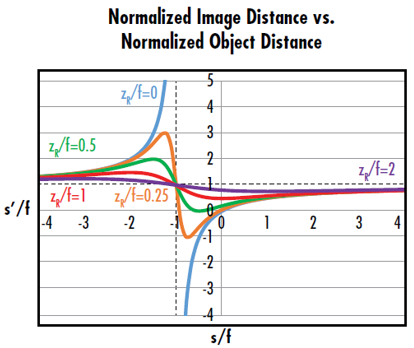
Figure 6: The curve where zR/f=0 corresponds to the conventional thin lens equation. The curves where zR/f>0 show that Gaussian imaging has minimum and maximum image distances defined by the Rayleigh range
In order to understand the beam waist and Rayleigh range after the beam travels through the lens, it is necessary to know the magnification of the system (α), given by:
Where w0 is beam waist before the lens and w0’ is the beam waist after the lens. The thin lens equation for Gaussian beams can then be rewritten to include the Rayleigh range of the beam after the lens (zR'):
The above equation will break down if the lens is at the beam waist (s=0). The inverse of the squared magnification constant can be used to relate the beam waist sizes and locations3:
Focusing a Gaussian Beam to a Spot
In many applications, such as laser materials processing or surgery, it is highly important to focus a laser beam down to the smallest spot possible to maximize intensity and minimize the heated area. In cases such as these, the goal is to minimize w0' (Figure 7). A modified version of Equation 13 may be used to identify how to minimize the output beam waist3:
Figure 7: Focusing a laser beam down to the smallest possible size is crucial for a wide range of applications including this laser cutting setup
After multiplying both sides by the denominator from the left side of the equation and then multiplying both sides by (w0')2, Equation 14 becomes:
Solving for w0' results in:
The focused beam waist can be minimized by reducing the focal length of the lens and |s|-f. The terms next to w0 in Equation 17 are defined as another form of the magnification constant α in order to compare the values of the input beam to the output beam after going through the lens (Figure 8).3
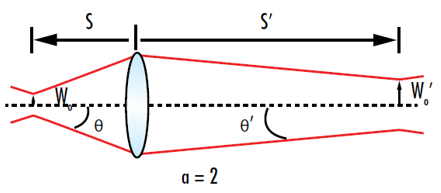
Figure 8: For a magnification of 2, the output beam waist will be twice the input beam waist and the output divergence will be half of the input beam divergence
There are two limiting cases which further simplify the calculations of the output beam waist size and location: when s is much less than zR or much greater than zR.3 When the lens is well within the laser’s Rayleigh range, then s << zR and (|s| − f)2 < zR2. Equation 18 simplifies to:
This also simplifies the calculations for the output beam’s waist, divergence, Rayleigh range, and waist location:
When s >> zR, the distance from the lens to the focused spot equals the focal length of the lens.
The other limiting situation where the lens is far outside of the Rayleigh range and s >> zR, simplifying Equation 18 to:
Which makes the output beam waist diameter:
Similarly to when s << zR, the calculations for the output beam waist, divergence, Rayleigh range, and beam waist location are also simplified:
When s >> zR, the distance from the lens to the focused spot equals the focal length of the lens.
Both of these results intuitively make sense because the beam’s wavefront is approximately planar both at and very far away from the beam waist. At these locations, the beam is almost perfectly collimated (Figure 9). According to the standard thin lens equation, a collimated input would have an image distance equal to the focal length of the lens.
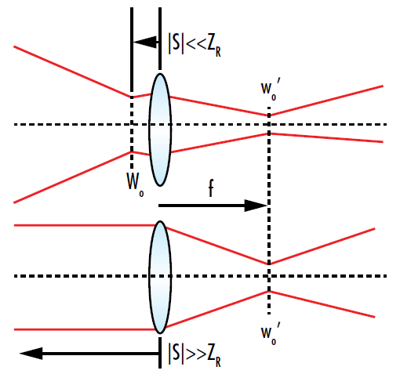
Figure 9: The focused spot of a Gaussian beam after it passes through a lens will be located at the focal point of the lens if the input beam waist is either very close or very far away from the lens. This is because the input beam is approximately collimated at those points
Gaussian Focal Shift
Counterintuitively, the intensity of a focused beam in a target at a fixed distance (L) away from the lens is not maximized when the waist is located at the target. The intensity on the target is actually maximized when the waist occurs at a location before the target (Figure 10). This phenomenon is known as Gaussian focal shift.
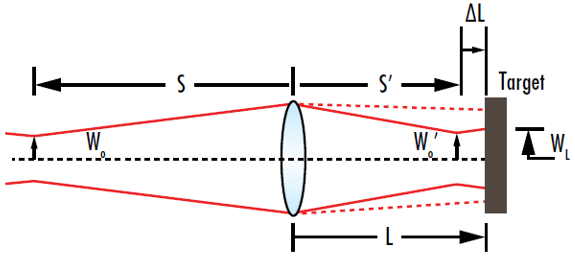
Figure 10: The minimum beam radius at a target occurs when the waist of the focused beam occurs at a specific location before the target, not when focused waist is located at the target
The lengthy derivation is not covered in this text, but the beam radius at the target can be described by the following expression4:
Differentiating Equation 34 with respect to the focal length of the focusing lens (f) and solving for f when d⁄df [wL (f )] = 0 reveals the lens focal length resulting in the minimum beam radius, and therefore highest intensity, at the target.
As |s| approaches either zero or infinity, d⁄df [wL (f )] = 0 when f = L. In both of these cases, the input beam is approximately collimated, and it thereby follows that the smallest beam radius would occur at the focal point of the lens.
Collimating a Gaussian Beam
Achieving a truly collimated beam where the divergence is 0 is not possible, but achieving an approximately collimated beam by either minimizing the divergence or maximizing the distance between the point of observation and the nearest beam waist is possible. Since the output divergence is inversely proportional to the magnification constant α, the output divergence reaches a minimum value when |s| = f (Figure 11).
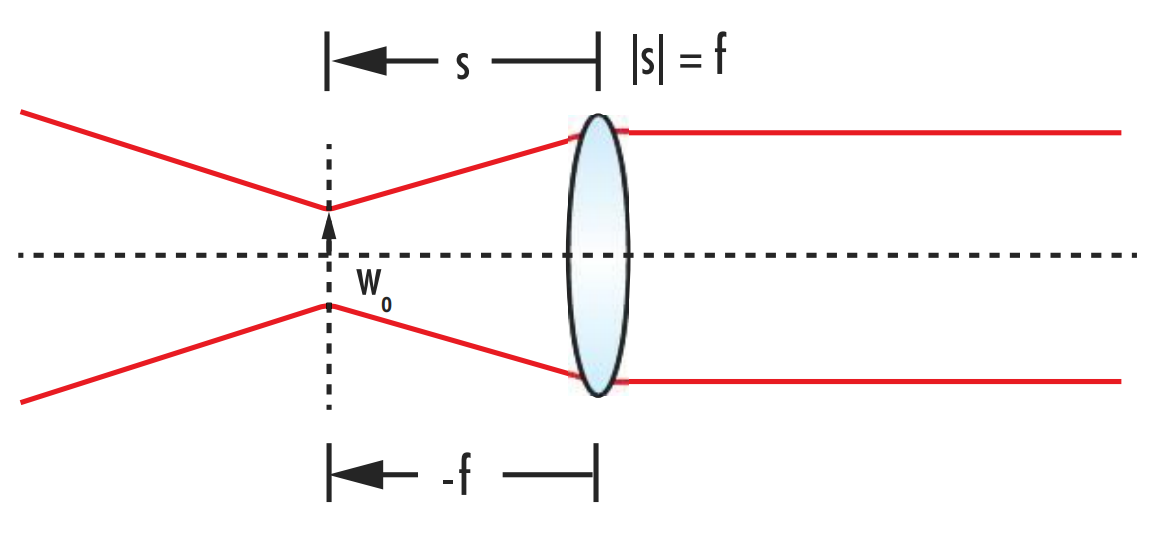
Figure 11: To collimate a Gaussian beam, the distance from the beam waist to the collimating lens should be equal to the lens’ focal length
References
- Paschotta, Rüdiger. Encyclopedia of Laser Physics and Technology, RP Photonics, October 2017, www.rp-photonics.com/encyclopedia.html.
- Self, Sidney A. “Focusing of Spherical Gaussian Beams.” Applied Optics, vol. 22, no. 5, January 1983.
- O'Shea, Donald C. Elements of Modern Optical Design. Wiley, 1985.
- Self, Sidney A. “Focusing of Spherical Gaussian Beams.” Applied Optics, vol. 22, no. 5, Jan. 1983.
- Katz, Joseph, and Yajun Li. “Optimum Focusing of Gaussian Laser Beams: Beam Waist Shift in Spot Size Minimization.” Optical Engineering, vol. 33, no. 4, Apr. 1994, pp. 1152–1155., doi:10.1117/12.158232.
More Resources













 Previous Section
Previous Section 





























































or view regional numbers
QUOTE TOOL
enter stock numbers to begin
Copyright 2023 | Edmund Optics, Ltd Unit 1, Opus Avenue, Nether Poppleton, York, YO26 6BL, UK
California Consumer Privacy Acts (CCPA): Do Not Sell or Share My Personal Information
California Transparency in Supply Chains Act